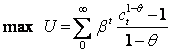Estado Estacionario

•  Estado Estacionario.

El estado estacionario es aquel punto donde todas las variables en términos per capita efectivo permanecen constantes, en forma simbólica:

Para que las variables en términos per capita permanezcan constantes, las variables deben crecer a la suma de las tasas a la que crece la población y el producto, en forma simbólica:

Utilizando la ecuación (12) obtenemos el capital per cápita de estado estacionario:

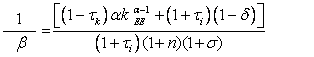
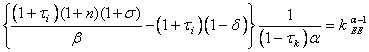
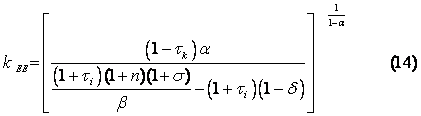
Alternativamente:

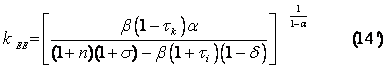
Si aumenta el impuesto al capital o el impuesto a la inversión el capital de estado estacionario disminuye:

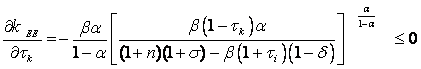
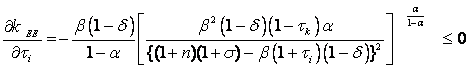
Comparando (14) con la solución de equilibrio pareteano, que se obtiene haciendo todas las alícuotas impositivas iguales a cero ( t c = t i = t l = t k = 0), esta economía con gobierno tiene un k menor al socialmente óptimo.

Equilibrio pareteano :

donde k EE < k p EE

Si remplazamos (14) en la función de producción, podemos obtener el producto per cápita de estado estacionario.

Como la producción depende directamente del capital per cápita, un aumento del impuesto al capital o a la inversión disminuirá la producción por trabajador efectivo.

Utilizando (11), (13), (14) y (15) obtenemos el consumo de estado estacionario.

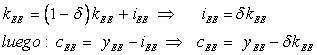
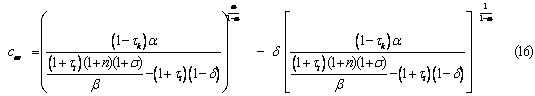
También se verifica que un aumento en los impuestos provoca una disminución del consumo per cápita.

La inversión de estado estacionario la obtenemos remplazando (14) en la condición de acumulación de capital:

El gasto público y las transferencias de estado estacionario se obtienen remplazando los resultados anteriores en la restricción presupuestaria del gobierno

.

Donde:

Un aumento de la alícuota al capital debería aumentar la retribución al mismo, mientras que disminuye el salario de estado estacionario. Esto es así ya que al aumentar la alícuota se desincentiva la acumulación de capital; ello implica una menor relación capital trabajo en el estado estacionario y por ende una menor tasa marginal de sustitución técnica entre los factores, llevando a que la productividad marginal del capital aumente y la del trabajo disminuya, con la consecuente redistribución de ingresos en favor del capital.

La tasa de ahorro en estado estacionario es:

De aquí surge que:

Por lo tanto cualquier aumento de las alícuotas a la inversión y/o la retribución al capital tienen un efecto regresivo sobre la propensión marginal al ahorro, como así también con respecto al ahorro total.

Esta conclusión puede llevar a pensar que en el modelo existe ULTRARRACIONALIDAD ; pero no es así. Ya que parte de lo recaudado con los impuestos es devuelto en transferencias, por lo que el ahorro global de la economía debe disminuír indefectiblemente (suponiendo que el gasto público es ahorro e inversión llevado a cabo por el estado).

Por otro lado, nada asegura que el aumento de la recaudación sea idéntico a la disminución del ahorro (inversión) privado(a). Inclusive se verá más adelante que los cambios de alícuotas tienen un "Laffer" sobre la recaudación tributaria.

Por otro lado, se puede observar que en ninguna de las ecuaciones de equilibrio derivadas hasta aquí aparecen las alícuotas de IVA o de las cargas sociales. Esto lleva a pensar que en este modelo simple (donde no existe elección entre ocio y trabajo) la mejor manera que tiene de recaudar el estado es a través de estos dos impuestos.

De esta forma no distorsiona los precios relativos de mercado, permitiendo que la economía no salga del equilibrio de Pareto (de algún punto de la línea de contrato).

A riesgo de ser repetitivo, cabe recordar que esto es válido sólo en el marco en donde el ocio no entra dentro de la función de utilidad; de esta forma el cambio en el precio relativo entre ocio y consumo (producto de cambios en las respectivas alícuotas) no alteran la desición de trabajo del agente representativo.