La función de producción linear es la mas simple de las funciones de producción: describe una relación linear entre los insumos y el producto.
Sólo un factor de producción
Si la función tiene sólo un factor, la misma se puede representar utilizando la siguiente fórmula:
y = a x
Por ejemplo, si un carpintero puede producir 10 sillas por día, la función de producción será:
Q = 10 L
Esta función de producción se puede representar utilizando el siguiente gráfico:
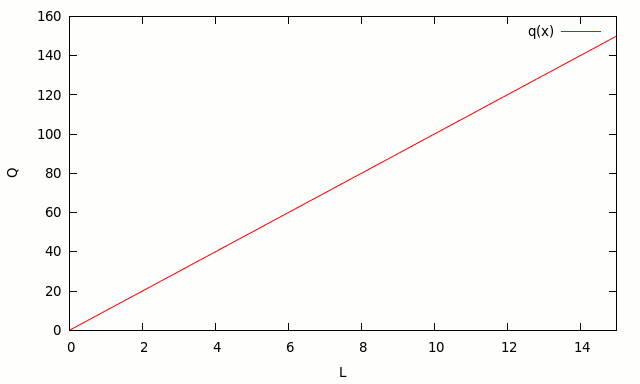
El coeficiente 10 representa la productividad del trabajo. Si el trabajador aumenta su productividad, porque tomó un curso para producir sillas mas eficientemente, por ejemplo, este coeficiente aumentará y la pendiente de la función de producción será mas elevada.
Múltiples factores de producción
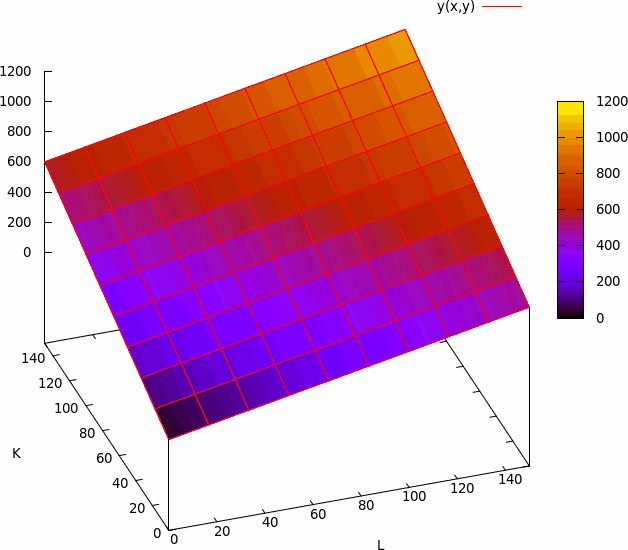
Si la función de producción tiene mas de un factor, se puede representar de la siguiente manera:
y = a1 x1 + … + an xn
Si visualización es la siguiente:
Isocuanta
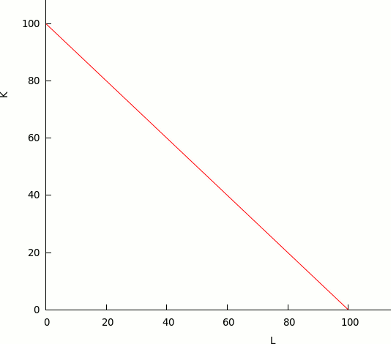
Considerando una función de producción de la siguiente forma:
Q = K + L
La misma tiene la siguiente isoquanta:
Elasticidad de sustitución
Podemos ver que la isocuanta es una linea recta, lo cual nos indica que los factores son sustitutos perfectos: manteniendo el mismo nivel de producción, pueden ser sustituídos unos por otros a una tasa que se mantiene constante en todo el rango.
La elasticidad de sustitución es una medida de cuán fácilmente puede un factor ses sustituido por otro. Matemáticamente, se define como el porcentaje del cambio en la proporción de los factores, dividido el cambio en la tasa marginal de sustitución técnica (TMST).
Para entender la misma en el caso de la función de producción linear, por favor observa el siguiente gráfico:
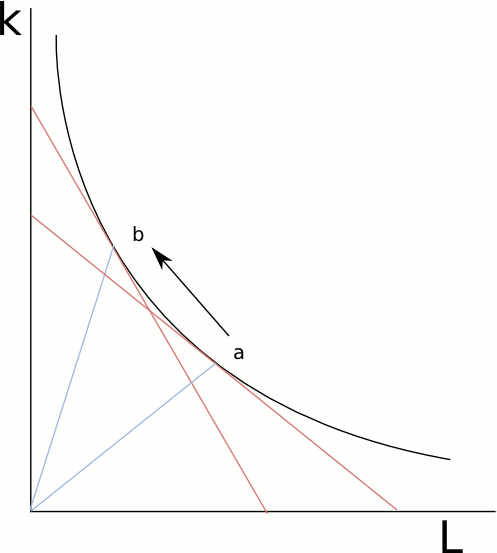
En el punto a, la pendiente de la tangente mide la TMST, es decir, cuánto L se puede disminuir ante un aumento infinitesimal de K, para que la producción se mantenga constante. Si nos movemos al punto b, la TMST aumenta.
La relación K/L se puede ver como la pendiente del rayo que va desde la ordenada de origen hasta el punto de la isocuanta en cuestión.
La TMST mide la relación entre el cambio en K/L y el cambio en la TMST.
Si la isocuanta es muy curva o cóncava, el cambio en la TMST es grande en relación al cambio en K/L: la elasticidad de sustitución es menor.
En el caso de la función de producción linear, la TMST se mantiene constante (el denominador de la fórmula de la elasticidad de sustitución es cero).
El cambio en K/L no es cero. Entonces, la elasticidad de sustitución es ∞.
Retornos a escala
Los retornos a escala miden la cuánto aumenta la producción, ante un cambio proporcional de todos los factores.
- Si el aumento es mas que proporcional, los retornos a escala son crecientes.
- Si el aumento es menos que proporcional, los retornos a escala son decrecientes.
- Si el cambio es proporcional, los retornos a escala son constantes.
La función de producción linear tiene retornos a escala constantes.
Para probar esta afirmación, multiplicamos todos los insumos por un factor c. Y’ representa el nuevo nivel de producción.
Y = aK + bL
Y’ = a (cK) + b (cL)
= c (aK + bL)
= c Y
Si todos los insumos aumentan en una proporción c, el prodcuto aumenta en c: la función de producción linear tiene retornos a escala constantes.
Ejemplos de función de producción linear:
- Un trabajador que produce 200 pizzas por día: Y = 200L
- Un carpintero que produce 10 sillas por día Y = 10L
- Un carpintero que produce 10 sillas por día y un robot que produce 20 sillas por día: Y = 10L + 20R
- Discos duros que almacenan 500GB y discos duros que almacenan 1000GB. La función de producción de capacidad de almacenamiento de datos es: Y = 500GB * A + 1000GB * B
zonaeconomica.com "Función de Producción Linear" [en linea]
Dirección URL: https://www.zonaeconomica.com/funcion-de-produccion/linear (Consultado el 27 de Feb de 2026)
Añadir nuevo comentario