Hola, mirá, no creo que la información que te vaya a dar sea suficiente como para presentar en un trabajo, pero te doy las ideas básicas.
Bueno, el modelo clásico que te voy a presentar es formalmente estático, es decir, las variables no van a estar fechadas. Elegimos esto para contrastar los resultados de una política monetaria expansiva del gobierno entre este modelo y el modelo "keynesiano" publicado por Hicks.
Primero impondremos los supuestos de este modelo.
(1)
Y = A * F ( L ; K )
Es decir, la producción agregada en esta economía cerrada (este es otro supuesto del modelo), depende de la productividad total de los factores (A) ó “tecnología” y de los factores de producción: trabajo (L) y capital (K). Esta función responde a las condiciones comunes: su primera derivada con respecto a cada uno de los factores es positiva, mientras la segunda es negativa. Es decir, aumentos tanto del trabajo como del capital producen un aumento en el producto, pero auna tasa decreciente (tienen productividades marginales decrecientes).
(2)
L = Ls ( W/P )
(3)
L = Ld ( W/P ; K )
Notemos que aquí estamos imponiendo el equilibrio en el mercado de trabajo. La ecuación (2) nos indica que la oferta de trabajo depende (positivamente) del salario real (W/P) y la (3) nos dice que la demanda de trabajo depende (negativamente) del salario real y (positivamente) de las existencias de capital. Aclaración: la demanda de trabajo de las firmas proviene de la condición de maximización de beneficios PRODUCTIVIDAD MARGINAL DEL TRABAJO = W/P, o sea, ?F/?L = W/P, lo que nos “grafica” la curva de demanda de trabajo que más tarde veremos en el mercado laboral.
(4)
Yd = C + I + G
Esta es la composición de la demanda agregada en nuestra economía que, como es “cerrada”, le falta el “+ XM” (exportaciones netas) para completar la ecuación que conocemos de la contabilidad nacional.
(5)
C = C ( Y – T ; r )
Aquí definimos al consumo como una función que depende del ingreso DISPONIBLE (Y – T, es decir, el ingreso que les queda a los individuos luego de descontar los impuestos del gobierno) y la tasa de interés real (r). El consumo depende positivamente de la primera de estas dos variables y negativamente de la segunda, ya que al aumentar r aumenta el costo de oportunidad consumir una unidad de consumo hoy, es decir, se da una especie de cambio en los precios relativos del consumo de hoy vs. el consumo de mañana. Recordemos que esto tiene vigencia en este modelo porque lo definimos FORMALMENTE estático, no estático (a secas).
(6)
I = I (r)
La inversión es función de la tasa de interés. Al igual que en caso del consumo, la inversión depende negativamente de la tasa de interés. Esto se debe a que el aumento de r significa un aumento del retorno de los bonos, por lo tanto, un aumento en el costo de oportunidad de la última unidad de capital “invertida”. Así, si aumenta r, muchos de los recursos destinados a la inversión irán a parar a los bonos por el motivo recién explicado.
(7)
M/P = ? ( r ; Y )
Esta es la condición de equilibrio en el mercado de dinero, ya que tomamos a M como la base monetaria u oferta de dinero del gobierno. Esto nos dice que la demanda real de dinero es una función que depende de la tasa de interés y el nivel de producto. Notemos que si bien el retorno de un bono es una tasa de interés nominal (i), estamos considerando a la tasa de interés real (r) ya que, como el modelo no es dinámico no podríamos hablar de Inflación (o Inflación esperada) porque nos estaría faltando el nivel de precios futuro (o esperado). Así, consideramos a la Inflación ? = 0, y como la ecuación de Fisher nos dice que i = r + ? entonces i = r. Es por esto que utilizamos r en lugar de i. La demanda real de dinero depende negativamente de la tasa de interés ya que un aumento en dicha tasa significa un aumento del costo de oportunidad de tener dinero en el bolsillo, por lo que la demanda de dinero disminuiría ante un aumento de dicha tasa. Por otro lado, un aumento en el nivel de producto lo podríamos pensar como un aumento en el nivel de transacciones en la economía, y para poder aumentar mi cantidad de transacciones aumentaré mi demanda de dinero.
Ahora tenemos todos los supuestos necesarios para esta economía que responde al modelo clásico.
Los gráficos siempre son una herramienta útil para guiarnos en el estudio de la estática comparativa.
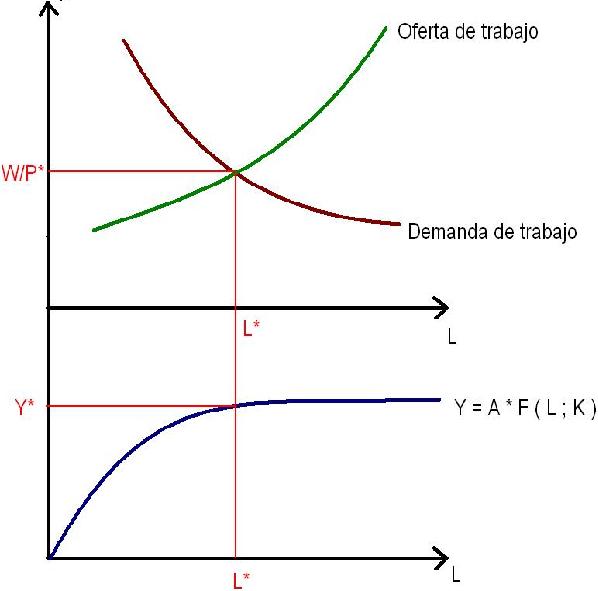
Así se determina el nivel de trabajo de esta economía, el salario real y, para un nivel dado (fijo) de capital, la oferta de bienes.
Faltan por ver los mercados de bienes y de dinero.
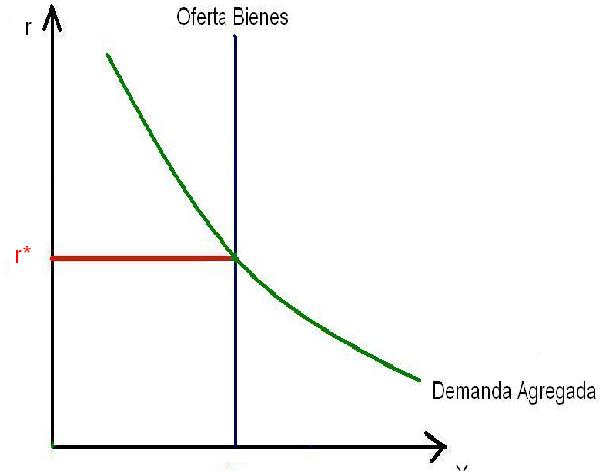
Este es nuestro mercado de bienes, donde oferta y demanda agregadas (recordemos que Yd = C + I + G y como C e I dependen negativamente de r y G es exógeno, la demanda agregada dependerá negativamente de la tasa de interés real, es por esto que tiene pendiente negativa) determinan conjuntamente la tasa de interés real de equilibrio. Notemos que la oferta agregada es vertical. ¿Por qué? Si bien la oferta de bienes depende del nivel de trabajo (y por ende del salario real) y del nivel de existencias de capital (o sea, del período “pasado”, por lo que K es exógeno, es un dato), no depende de ninguna forma de la tasa de interés r. Por lo tanto, si graficamos Y “contra” r, la oferta agregada de bienes será una recta vertical que determinará el nivel de producto. (Nota: en los modelos de economías con un horizonte temporal de 2 o más períodos, si la función de producción depende del trabajo no será una recta sino una curva con pendiente positiva debido al efecto sustitución intertemporal que variaciones de r generan sobre la oferta de trabajo de período presente).
Por último analizaremos el gráfico del mercado de dinero.
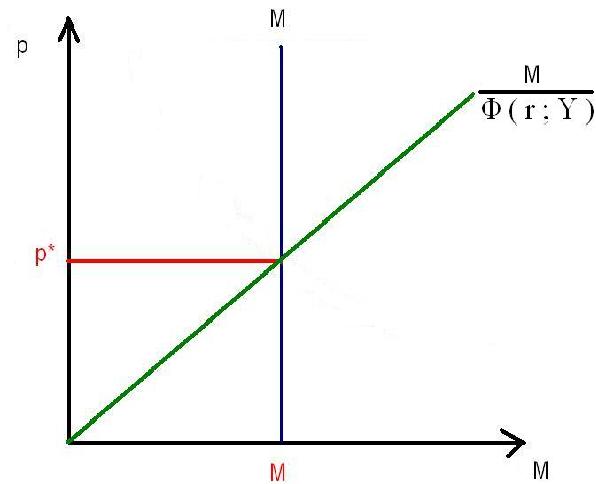
La oferta de dinero (M) es una variable exógena para esta economía, por lo que, análogamente al caso de la oferta agregada en el mercado de bienes, será una recta vertical. La demanda de dinero está dada por la ecuación (7) que analizamos más arriba. En este mercado, oferta y demanda determinarán conjuntamente el nivel de precios de esta economía.
Veamos qué sucede cuando el gobierno decide aumentar la oferta monetaria (aumenta M à M ’ > M ). “M” solo aparece en la última ecuación de las siete de nuestro modelo. Es decir, un aumento en M provocará únicamente (por ahora) variaciones en el mercado de dinero. Gráficamente:
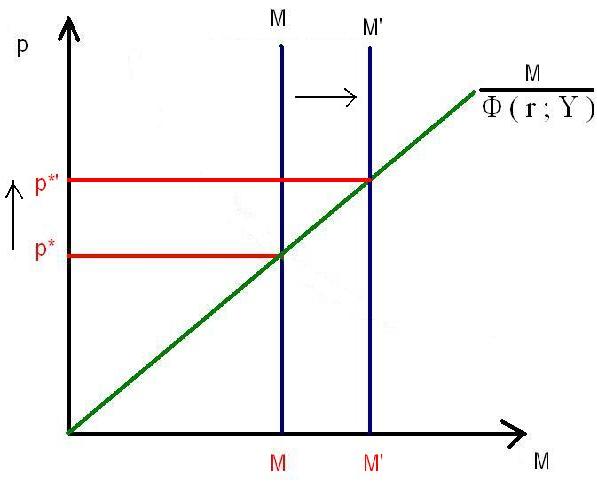
Como el gráfico nos enseña, un aumento en M provocará un aumento en el nivel de precios de la economía en la misma proporción dado que, como la demanda real de dinero (?) no sufrió modificaciones pues no variaron ni r ni Y, el cociente M/P deberá permanecer constante para satisfacer la condición de equilibrio de este mercado (ecuación (7)).
Ahora bien, el aumento de M produce un aumento en P, y el aumento en P… ¿qué produce? La intuición nos dice que dado que aumentó el nivel de precios, el salario real deberá caer, por lo que el mercado laboral se verá afectado por la política expansiva del gobierno y, así, también el mercado de bienes (dado que la oferta agregada depende del nivel de trabajo). Sin embargo esta intuición es errónea en este modelo donde los salarios nominales (W) son flexibles. Es decir, no habrá cambios en el salario real porque el salario nominal aumentará en la misma proporción que el nivel de precios para, así, dejar al cociente W/P en la misma situación que antes del aumento en M.
Finalmente, podemos concluir que en el marco del modelo clásico, con salarios nominales flexibles, una política monetaria expansiva del gobierno no genera variaciones en las variables reales de la economía, entre ellas la más importante el nivel de producto: Y.
Bueno, espero que te haya servido esto. Sé que no estoy contestando a todo lo que pedís así que si necesitás algo más decime a ver si te puedo ayudar y además avisame si ERA ESTO LO QUE PEDÍAS! jajaja...
Saludos. Francisco.