En este apartado se presentan los cálculos y algoritmos realizados para simular diferentes impactos en la economía, mas precisamente en el producto y en el nivel de precios, impulsados por la política fiscal, la política monetaria, o bien cambios estructurales tales como avances tecnológicos, como también cambios en la preferencia por la liquidez por parte de los agentes económicos.
En primer lugar se presenta un equilibrio inicial para ciertos valores de los parámetros. Aquí se presentan en las funciones demanda_agregada1(Pd) y oferta_agregada1(Po), siendo Pd y Po los correspondientes precio de demanda y oferta a nivel agregado . La función exceso_demanda calcula (DA – OA) de la situación inicial. La función precio_de_equilibrio(.), calcula el cero de la función anterior usando el solver de Matlab fzero ,obteniendo como salida de maquina el precio de equilibrio.
%==================Calculo de la Demanda Agregada =======================
function [qd] = demanda_agregada1(Pd)
A0=1400;
l0=0.1;
l1=10;
alpha=4;
I1=20;
M0=10000;
qd = (l1*alpha ./(l1+ alpha*I1*l0))* A0 + (I1*alpha ./(l1 + alpha*I1*l0))* M0 ./Pd
%===================Calculo de la Oferta Agregada ======================
function [qo]=oferta_agregada1(Po)
A=100;
beta=0.6;
W=5
qo =A*((beta*A*Po)./W).^(beta ./(1- beta))
====================Función Exceso de demanda ===========================
function [excd]=exceso_demanda(P)
excd = demanda_agregada1(P) - oferta_agregada1(P)
%===================Calculo del precio de equilibrio ==================
%Para encontrar el precio de equilibrio calculamos los ceros de la
%función exceso de demanda
function [pe] = precio_de_equilibrio(a)
pe = fzero( 'exceso_demanda' ,a)
%============Figura(1): Cantidad y precio de equilibrio iniciales ======
function [x] = grafico_oada(a,b,N)
P=linspace(a,b,N)'
for i=1:N
da(i) = demanda_agregada1(P(i));
oa(i) = oferta_agregada1(P(i));
end
plot(da,P,oa,P)
title( 'Cantidad y Precio de Equilibrio de la economía' )
ylabel( 'Nivel de Precio' )
xlabel( 'Cantidad' )
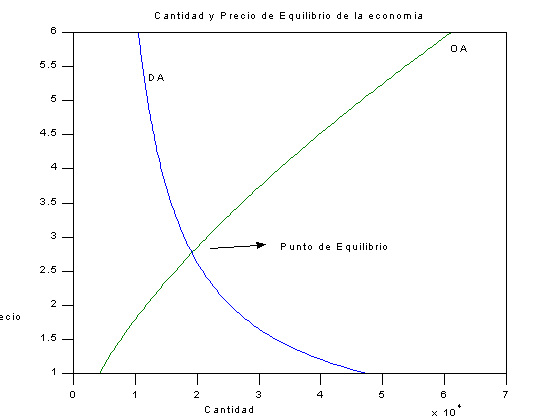
III.1) Cambio en el Componente Autónomo del Gasto (Ao)
Aquí se presenta el nuevo nivel de equilibrio (Precio y Cantidad) que se alcanza luego de un cambio en el gasto autónomo de la demanda agregada. Particularmente puede interpretarse el efecto de una política fiscal expansiva llevada a cabo a través de un aumento del Gasto Público. Mismo efecto tendría, a través del multiplicador, cualquier variación en la inversión y consumo autónomos, como también un cambio en el nivel de las exportaciones netas.
La modificación se introduce en la función demanda agregada, como así también en las funciones exceso_demanda(.) y precio_de_equilibrio(.) . Mas precisamente:
function [qd] = demanda_agregada3(Pd)
%efectos de un aumento en el componente autónomo del Gasto
%Esto puede deberse a una política fiscal expansiva de 1000
%o equivalentemente un aumento en las exportaciones o en la inversión autónoma
A1=2400;
l0=0.1;
l1=10;
alpha=4;
I1=20;
M0=10000;
qd = (l1*alpha ./(l1+ alpha*I1*l0))* A1 + (I1*alpha ./(l1 + alpha*I1*l0))* M0 ./Pd
%============Figura(2): Política Fiscal Expansiva ====================
function [x] = grafico_gastoA(a,b,N)
P=linspace(a,b,N)'
for i=1:N
da1(i) = demanda_agregada1(P(i));
oa(i) = oferta_agregada1(P(i));
da3(i) =demanda_agregada3(P(i));
end
plot(da1,P,oa,P,da3,P)
title( 'Efectos de una Política Fiscal Expansiva mediante aumento del Gasto Publico' )
ylabel( 'nivel de precio' )
xlabel( 'Cantidad' )
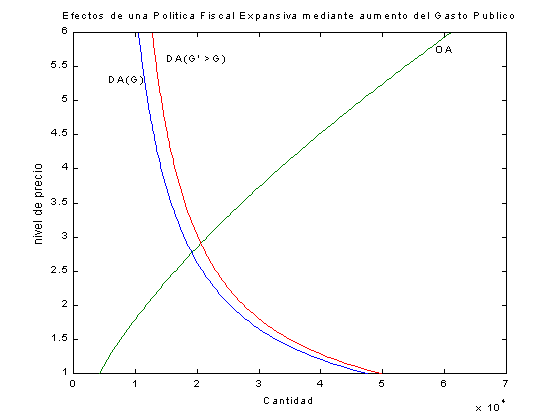
De aquí se ve el efecto expansivo de estimular la demanda agregada a través del gasto público.
III. 2) Aumento en al alícuota impositiva : Política Fiscal Contractiva
En la situación inicial se tiene un multiplicador del gasto igual a 4. Esto viene de valores de c =0.75, t =1/3y m=0.25
Supongamos un aumento en la alícuota impositiva hacia el valor t´=2/3
Para esto usamos la nueva función de demanda agregada, demanda_agregada2, esceso_demanda2, precio_de_equilibrio2 y queda graficado en grafico_impuesto.
function [qd]=demanda_agregada2(Pd)
%efecto de un aumento en la alícuota impositiva
%este se expresa a través del multiplicador alpha= 1/1-c*(1-t)+ m, dejándolo igual a 2
%siendo c la prop. mg a consumir,t la alícuota impositiva y m la prop. Mg. a importar
A0=1400;
l0=0.1;
l1=10;
alpha2=2;
I1=20;
M0=10000;
qd = (l1*alpha2 ./(l1+ alpha2*I1*l0))* A0 + (I1*alpha2 ./(l1 + alpha2*I1*l0))* M0 ./Pd
%============Figura(3):Política Fiscal Contractiva ====================
function [x] = grafico_impuesto(a,b,N)
P=linspace(a,b,N)'
for i=1:N
da1(i) = demanda_agregada1(P(i));
oa(i) = oferta_agregada1(P(i));
da2(i) =demanda_agregada2(P(i));
end
plot(da1,P,oa,P,da2,P)
title( 'Efectos de una Política fiscal Contractiva mediante aumento de la alícuota impositiva' )
ylabel( 'Nivel de Precio' )
xlabel( 'Cantidad' )
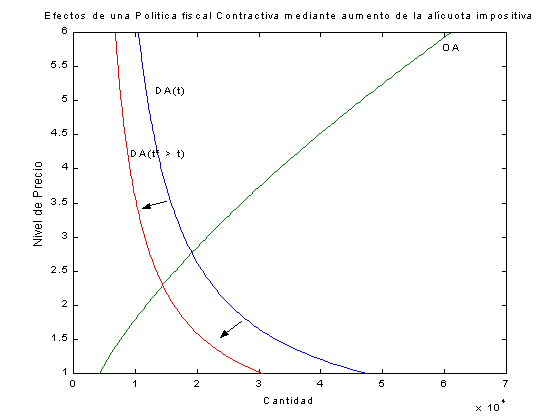
III.3) Política Monetaria Expansiva
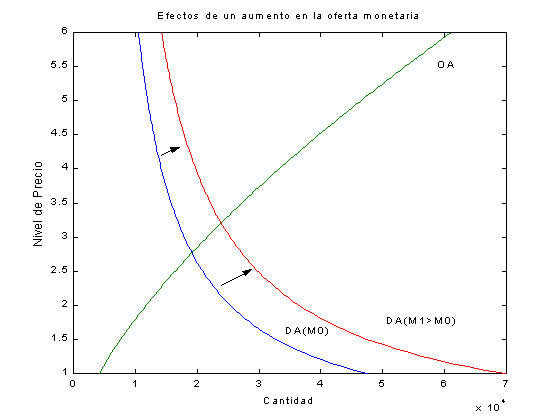
Aquí la política monetaria expansiva se observa en el aumento la oferta monetaria de M0 = 10000 a M1 =15000, desplazando así la demanda agregada.
Se puede ver la efectividad de la política monetaria en aumentar el producto de equilibrio de la economía, dados la especificación de los parámetros. Del mismo modo, se observa el aumento en el nivel general de precios que deviene de esta política, cumpliéndose así la proposición cuantitativista.
function [qd] = demanda_agregada5(Pd)
%efectos de una política monetaria expansiva
A1=1400;
l0=0.1;
l1=10;
alpha=4;
I1=20;
M1=15000;
qd = (l1*alpha ./(l1+ alpha*I1*l0))* A1 + (I1*alpha ./(l1 + alpha*I1*l0))* M1 ./Pd
============Figura(5): Efectos de una Política Monetaria expansiva ======
function [x] = grafico_monetaria(a,b,N)
P=linspace(a,b,N)'
for i=1:N
da(i) = demanda_agregada1(P(i));
oa(i) = oferta_agregada1(P(i));
da5(i)= demanda_agregada5(P(i));
end
plot(da,P,oa,P,da5,P)
title( 'Efectos de un aumento en la Base Monetaria' )
ylabel( 'Nivel de Precio' )
xlabel( 'Cantidad' )
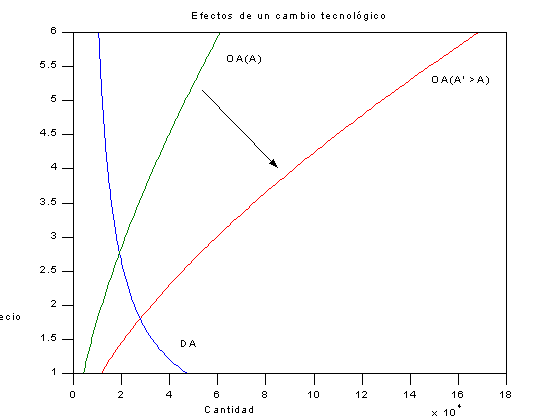
III.4) Efectos de un Cambio Tecnológico
En los apartados anteriores se observaron movimientos en la curva de DA , ahora observaremos un cambio sobre la Oferta Agregada , provocado por un cambio en el parámetro tecnológico A .Aquí se ve una expansión en el producto de equilibrio junto con una caída en el nivel de precios, violando así la hipótesis de la curva de Phillips lo cual es propio del largo plazo.
function [qo]=oferta_agregada2(Po)
%efectos de un cambio tecnológico sobre la producción y el nivel de precios
A=150;
beta=0.6;
W=5
qo=A*((beta*A*Po)./W).^(beta ./(1- beta))
%==========Efecto de un cambio Tecnológico =======================
function [x] = grafico_tecnologia(a,b,N)
P=linspace(a,b,N)'
for i=1:N
da1(i) = demanda_agregada1(P(i));
oa1(i) = oferta_agregada1(P(i));
oa2(i) = oferta_agregada2(P(i));
end
plot(da1,P,oa1,P,oa2,P)
title( 'Efectos de un cambio tecnológico' )
ylabel( 'Nivel de Precio' )
xlabel( 'Cantidad' )
En todos estos puntos se trabajó con funciones de demanda y oferta agregada separadas para cada nivel distintos de los parámetro, dejando a esta solo como función del precio. Alternativamente las funciones principales pueden programarse con un nivel mayor de generalidad, es decir, generalizando para los valores de A0, l0, l1, I1, alpha, M0, W, beta y A. De este modo se puede trabajar con las siguientes funciones:
%============== Función de Demanda Agregada General =====================
function [qd] = demanda_agregada(A0,l0,l1,alpha,I1,M0,Pd)
if l1+ alpha*I1*l0 ==0 break
else
qd = (l1*alpha ./(l1+ alpha*I1*l0))* A0 + (I1*alpha ./(l1 + alpha*I1*l0))* M0 ./Pd
end
%================== Oferta Agregada General =============================
function [qo]=oferta_agregada(A,beta,W,Po)
if W==0 break
else
qo=A*((beta*A*Po)./W).^(beta ./(1- beta))
end
%==================== Función Exceso de Demanda =========================
function [excd]=ex_demanda(P)
excd = demanda_agregada(P) - oferta_agregada(P)
%===================== Precio de Equilibrio =============================
function [x] = p_de_equilibrio(a)
pe = fzero( 'exceso_demanda' ,a)
III.5) Efectividad de la Política Fiscal
Ahora se realizará una comparación de dos situaciones distintas, reflejadas en el valor del parámetro l1 (sensibilidad de la demanda de dinero ante cambios en la tasa de interés, en la respuesta de una política fiscal expansiva. Estas dos situaciones serían:
• Una economía caracterizada por una tener una sensibilidad de la demanda de dinero al tipo de interés relativamente pequeño (l1 ® 0), y por lo tanto, el multiplicador de la política fiscal ( Mf ) tendería a ser nulo.
• Una economía con un l1 significativamente grande (l1 ® ¥ ), donde en este caso el multiplicador de la política fiscal tiende al multiplicador del modelo keynesiano basico ( Mf ® a ).
%================== Efectividad de la Política Fiscal ===================
function [x] = grafico(a,b,N)
P=linspace(a,b,N)'
for i=1:N
da1(i) = demanda_agregada(1400,0.1,100,4,20,10000,P(i));
da2(i) = demanda_agregada(1400,0.1,2.5,4,20,10000,P(i));
da3(i) = demanda_agregada(5000,0.1,100,4,20,10000,P(i));
da4(i) = demanda_agregada(5000,0.1,2.5,4,20,10000,P(i));
oa(i) = oferta_agregada(150,0.6,5,P(i));
end
plot(da1,P,oa,P,da2,P,da3,P,da4,P)
title( 'Efectividad de la politica fiscal' )
ylabel( 'Nivel de Precio' )
xlabel( 'Cantidad' )
legend( 'da con un l1=100, y A0=1400' , 'oa' , 'da2 con I1=2,5 y A0=1400' , 'da3 con I1=100 con politica fisca expansiva(A0=5000)' , 'da4 con l1=2.5 y Politica fical expansiva' )
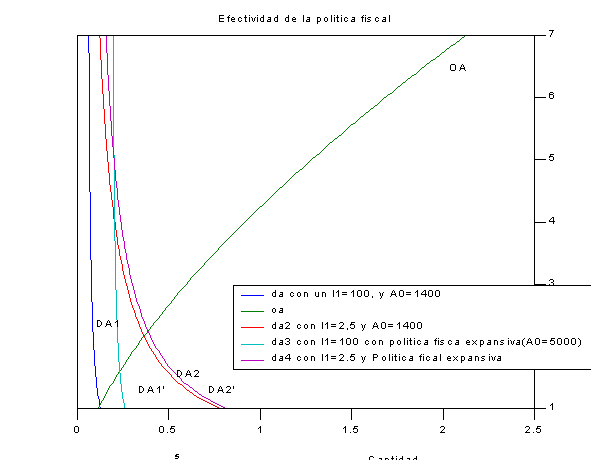
De este modo se puede ver como la política fiscal deja de ser efectiva a medida l1 tiende a valores “pequeños”, mientras que la efectividad aumenta para valores mayores de este.
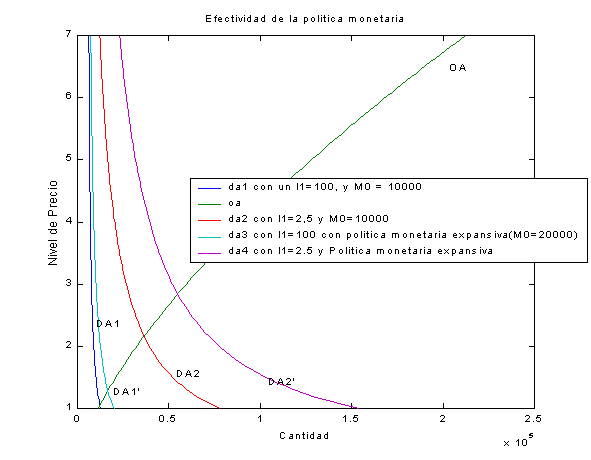
III.6) Efectividad de la Política Monetaria
Con las mismas dos situaciones que en el caso anterior, aquí vamos a poder observar que la efectividad de la política monetaria también varía con diferentes l1.
De aquí va resultar que para valores “pequeños” de l1 la política monetaria es efectiva, ocurriendo lo contrario cuando este es grande.
Así vemos como se revierte la situación anterior. Ahora tenemos lo siguiente:
%============Efectividad de la Política Monetaria============
function [x] = grafico(a,b,N)
P=linspace(a,b,N)'
for i=1:N
da1(i) = demanda_agregada(1400,0.1,100,4,20,10000,P(i));
da2(i) = demanda_agregada(1400,0.1,2.5,4,20,10000,P(i));
da3(i) = demanda_agregada(1400,0.1,100,4,20,20000,P(i));
da4(i) = demanda_agregada(1400,0.1,2.5,4,20,20000,P(i));
oa(i) = oferta_agregada(150,0.6,5,P(i));
end
plot(da1,P,oa,P,da2,P,da3,P,da4,P)
title( 'Efectividad de la politica monetaria' )
ylabel( 'Nivel de Precio' )
xlabel( 'Cantidad' )
legend( 'da1 con un l1=100, y M0 = 10000' , 'oa' , 'da2 con I1=2,5 y M0=10000' , 'da3 con I1=100 con politica monetaria expansiva(M0=20000)' , 'da4 con l1=2.5 y Politica monetaria expansiva' )
zonaeconomica.com "Simulación con Matlab" [en linea]
Dirección URL: https://www.zonaeconomica.com/matlab/ofertademanda/simulacion (Consultado el 12 de Mar de 2026)
Comentarios
Re: Simulación con Matlab
¿por qué no se puede correr tal cual en matlab? cuánto vale Pd y Po??
Añadir nuevo comentario