Interés Simple e Interés Compuesto

Autor: Lic. Pablo DÍAZ ALMADA - Septiembre 2009

En el sector financiero encontramos dos grupos de agentes económicos o unidades financieras, aquellos que presentan un excedente en sus necesidades de fondos (unidades ahorradoras) y aquellos que muestran fondos insuficientes para sus necesidades (unidades deudoras). El sector financiero posibilita, a través de las operaciones financieras, que las unidades ahorradoras se desprendan de su excedente de fondos para utilizarlo en su consumo futuro y tal excedente canalizarlo hacia las unidades deudoras que cuentan con fondos insuficientes por su deseo de incrementar su consumo presente.

Este capital financiero, propiedad de las unidades ahorradoras, presta un servicio por el cual hay que pagar. Por lo que se llama interés al incremento de capital que reciben las unidades ahorradoras como parte de pago de los servicios prestados por su capital financiero. Y también, viéndolo del lado de las unidades deudoras, el interés es el monto que debe pagarse por gozar del servicio del capital financiero prestado.

Podemos decir que toda operación financiera cuenta con los siguientes elementos:
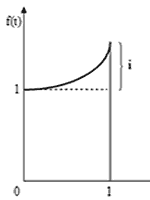
- El capital financiero [f(t)] que es el monto en efectivo valuado en una moneda particular del que se desprende la unidad ahorradora y del que toma una unidad deudora.
- El período de tiempo (t) por el cual el capital financiero prestará su servicio, llamando unidad de tiempo al período al final del cual se computan los intereses para ser cobrados, pagados o capitalizados.
- La tasa de interés (i) es la tasa de incremento de una unidad de capital en una unidad de tiempo, denominando interés al incremento total del capital financiero. La misma puede expresarse en tanto por uno (ej: 0,05 anual) o en porcentaje (ej: 5 % anual).

Los cuales podemos graficar:

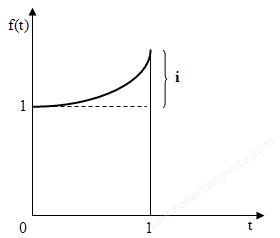
Para calcular el interés podemos describir diferentes métodos.

Interés simple

Esta forma de cálculo se caracteriza por generar intereses para todos lo períodos en base al capital inicial. Con lo cual, los intereses período a período son siempre los mismos.

I(f) = f(0) x i t = 1, 2, ..., n

Veamos con un ejemplo cómo se desarrolla su cálculo a lo largo de una inversión. Suponiendo un capital inicial f(0) = $ 15.000, invertido en un plazo n = 6 meses, a una tasa de interés i = 3 % mensual.

Mes	Capital al comienzo	Intereses	Capital al final
1	f(0) = 15000	        450	        f(1) = 15450
2	15450	                450	        f(2) = 15900
3	15900	                450	        f(3) = 16350
4	16350	                450     	f(4) = 16800
5	16800	                450     	f(5) = 17250
6	17250	                450     	f(6) = 17700
Total Intereses	2700	

Interés compuesto

Los intereses generados se acumulan al capital para producir nuevo interés en los períodos sucesivos. Por lo que, si no se retiran, el monto de interés generado período a período es cada vez mayor.

I(f) = f(t) x i t = 1, 2, ..., n

Veamos con el mismo ejemplo tomado anteriormente cómo se desarrolla el cálculo a lo largo de la inversión.

Mes	Capital al comienzo	Intereses	Capital al final
1	f(0) = 15000,00	        450,00       	f(1) = 15450,00
2	15450,00	        463,50     	f(2) = 15913,50
3	15913,50	        477,41   	f(3) = 16390,91
4	16390,91	        491,73	        f(4) = 16882,63
5	16882,63	        506,48   	f(5) = 17389,11
6	17389,11	        521,67	        f(6) = 17910,78
Total Intereses	2910,78	

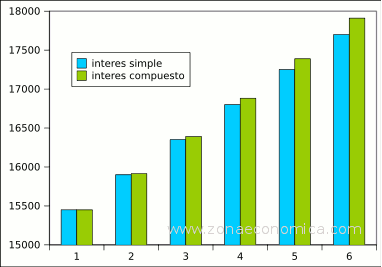
En el siguiente gráfico podemos comparar el interés simple con el interés compuesto:

©www.zonaeconomica.com
http://www.zonaeconomica.com/interes
Autor: Lic. Pablo DÍAZ ALMADA - Septiembre 2009

Referencias
Carrizo, J. F. (1972) "Conceptos básicos de matemática financiera." Asociación Cooperadora de la Facultad de Ciencias Económicas. Córdoba. Argentina.