
(Teoría de Juegos y Elección Racional)
Por: Axel Chávez Gódinez
Introducción
Desde la publicación de “Theory of games and economicbehavior” por John Von Neumann y la Tesis “Non “The Median Voter Theorem, Teoría de juegos aplicada” cooperativegames” del Dr. John Nash, la teoría de juegos ha ido trascendiendo del campo económico a otras ciencias como la Biología y las Ciencias sociales en general, entre estas últimas, las Ciencias Políticas no se han quedado atrás. A tal grado que ya han aparecido en escena los primeros modelos de teoría de juegos con aplicaciones al análisis político, entre los existentes con aplicación a la política el más conocido:”The Median VoterTheorem”, es un modelo sustentado por supuestos bastante básicos, por lo que en la siguiente disertación, me daré a la tarea de cambiar dichos supuestos, para crear un modelo más cercano a la realidad, siguiendo estrictamente la lógica económica impresa en teoría de juegos.

La idea principal de este modelo es que las ideologías políticas se encuentran organizadas en una escala del uno al diez y que existe también una población de votantes uniformemente distribuida en dicha escala, los jugadores son dos candidatos (J 1, J2) cuyo conjunto de estrategias (A1, A2) es comprendido por todos los números enteros del uno al diez, esto significa que, pueden elegir jugar una ideología, la cual les brindará un pago. De acuerdo al supuesto de que los votantes votan por el candidato cuya posición política sea la más cercana a la suya, el beneficio del “jugador i” estará dado por el número de votos que dicho candidato consigue (ver Figura 1.1).
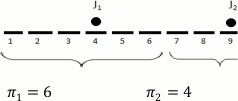
Figura 1.1: imagen muestra la situación en la cual el J1 utiliza su estrategia "4" mientras el J2 juega su estrategia "2"
Para proceder nuestro análisis habrá que encontrar, el o los equilibrios de Nash del juego, para ello será necesario realizar una eliminación de estrategias estrictamente dominadas para el “J i” por ambos extremos de la recta. Comenzaremos por eliminar las estrategias 1 y 10 al no ser mejores Figura 1.2: Eliminación iterativa de estrategias estrictamente dominadas respuestas (BR) para ninguna otra estrategia, una vez realizada esta eliminación, las estrategias 2 y 9 son ahora estrictamente dominadas, por lo que también son eliminadas y así sucesivamente hasta que solamente tengamos las estrategias 5 y 6, llegados a este punto, utilizaremos funciones de mejor respuesta:
BRi(5) = 5.6
BRi(6) = 6.5
Por medio de las funciones de mejor respuesta podemos afirmar que los equilibrios de Nash del juego son: (5,6), (6,5), (6,6), (5,5).
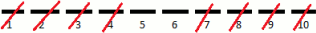
Este equilibrio es bastante estudiado por politólogos y asesores políticos ya que claramente muestra las ventajas de que un candidato adquiera una postura “central” durante una elección. Sin embargo del teorema del votante mediano (traducción al español del nombre del modelo), se desprenden otros modelos similares, como el que ahora procederemos a explicar.
Votantes en una distribución uniforme y continua
Una Variante, del teorema del votante mediano, que ocupará ahora nuestra atención es donde la recta que representa las posiciones políticas (en la cual se encuentra la población de manera uniforme) es una recta continua que va de cero a uno esto significa que ahora en lugar de analizar un número de votos, los pagos de los candidatos estarán dados en función del porcentaje de votos que cada uno recibe, sin embargo los jugadores ya no son solamente 2 sino que serán cualquier número real en el intervalo [0,1] ósea existe un número infinito de jugadores y las estrategias ya no son una postura política, sino la decisión de postularse o no, ello bajo el supuesto de que en las elecciones los candidatos no pueden elegir su postura ideológica sino que la van acarreando. La función de pagos es de la forma siguiente:

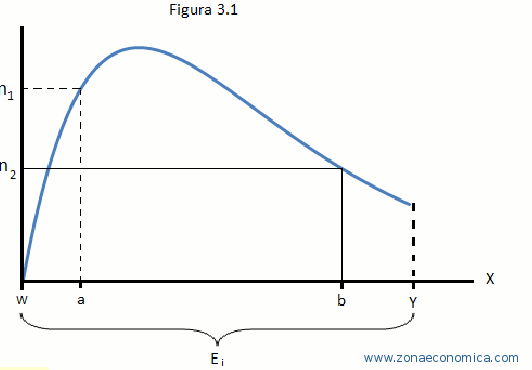
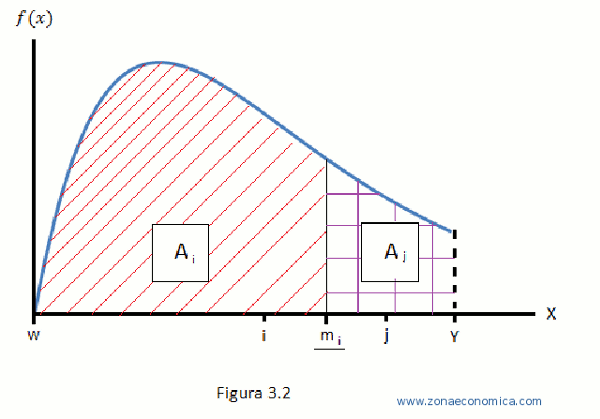
Como podemos darnos cuenta, cualquier estrategia que sigan los jugadores les brinda un beneficio (no necesariamente positivo), en el caso de ganar la elección J i recibe “a” (donde 0 Al igual que en el teorema del votante mediano, las estrategias son elegidas de manera simultánea, sin embargo, en este juego cada jugador evalúa su expectativa de ganar y decide postulase o no. La expectativa de ganar de cada jugador está dada por la creencia que tiene el jugador sobre los candidatos a postularse, para ilustrar esto fijémonos en la figura 2.1, donde ilustramos los equilibrios de Nash más sencillos del juego. Antes de continuar creo pertinente adelantar que este juego tiene infinidad de equilibrios de Nash y todos los resultados contenidos en la figura 2.1 Cumplen con la definición de Equilibrio De Nash. Comencemos con el primer resultado de la imagen: evidentemente J1 ganó la elección, si cualquier otro jugador hubieran entrado a la contienda habría pagado el costo de campaña más “D”, por lo tanto no es una elección racional para cualquier otro jugador contender contra J1, en el segundo caso, existe un empate por lo que ningún jugador tiene pérdidas ni ganancias, supongamos que el jugador que se ubica en la posición: 1/3 - k (donde 0 ≤ k ≤ 1/6) decide postularse, entonces el jugador en la posición 2/3 + k deberá también postularse, de lo contrario no jugaría su mejor respuesta, por otro lado, cualquier otro jugador distinto de "1/3 - k" y "2/3 + k" (ósea que no pertenezca a las parejas “1/3 - a" y "2/3 + a" donde a ε k ), no tiene incentivos a postularse, ya que de lo contrario enfentraría el costo "c" y ocasionaría la derrota en las elecciones del candidato más cercano a él si el jugador del que hablamos se ubica en el intervalo [ 0 , 1/3 ) ∩ (2/3, 1], por lo tanto las situaciones donde solamente se postulan las parejas de candidatos ubicados en la posiciones "1/3 - k" y "2/3 + k" Nash, en nuestra figura, la pareja 1/3 , 2/3 cumple esta condición, por lo tanto es un equilibrio de Nash. Si k ≥ 1/3 caemos en la situación del tercer ejemplo de la figura 2.1. No hace falta un análisis más intensivo para darnos cuenta de la existencia de múltiples equilibrios de Nash, sin embargo lo rescatable en el modelo, para motivos de nuestra investigación no es este hecho, sino más bien, son un conjunto de elementos presentes en el modelo que caben resaltar, en primer lugar se encuentra el hecho de manejar una recta continua, ya que trabajar con números reales es más exacto al momento de catalogar las posiciones, además, utilizar una recta es más cómodo (como veremos a continuación). La idea de que los candidatos busquen maximizar el porcentaje de votos, es algo que también nos será de utilidad. Por último, una observación que espero no haya pasado desapercibida al lector, es el hecho de que salvo la situación en la que solo se postula un jugador, los demás equilibrios de Nash no tienen un ganador en lo que respecta a la elección, esto es muy importante ya que para lograr el equilibrio de Nash (en nuestro juego) es necesario que todos los agentes sean racionales y libres de cualquier clase de limitaciones, lo cual casi nunca se cumple. asta ahora, el supuesto más fuerte en los modelos que hemos analizado, es el de la distribución uniforme de la población, sin embargo, en la vida real no existe población que no se encuentre concentrada en torno a una moda, teniendo en cuenta este aspecto debemos crear un nuevo modelo de elecciones que nos permita poder trabajar con poblaciones que se encuentres sesgadas. Los sesgos con los que trabajemos en el modelo, se encontrarán en torno a un conjunto de posturas políticas que guarden relativa cercanía. Ahora nos debemos darnos a la tarea de encontrar una manera de distribuir a la población en torno a las posturas políticas, para ello la siguiente afirmación será el supuesto fundamental del siguiente modelo: Para comenzar a ilustrar el modelo (ver figura 3.1), Supongamos que el conjunto de posturas políticas (Ei) se encuentra en un intervalo [w, y] sobre una recta continua, eso significa que un punto “a” ε Ei, representa la posición de una determinada postura sobre la recta (solamente los jugadores considerarán Ei como un conjunto de estrategias). Para ese punto “a” existe un determinado número de seguidores “n1”los cuales (por nuestro supuesto principal) comparten un nivel socioeconómico igual en la sociedad. Antes de continuar en la explicación del modelo, considero importante enfatizar, que la dispersión empleada en la figura 3.1, es solamente hipotética y salvo alguno que otro ejemplo, las premisas que mencionaré son aplicables a cualquier dispersión. En el conjunto Ei (para el caso de una dispersión con sesgo a la derecha como en la figura 3.1), resaltemos una postura “b” tal que b > k donde k es la postura que representa la mediana de la dispersión, notamos claramente que en escala a < b y que el número de seguidores de b “n2” , cumple que n1> n2, esto es una afirmación muy fuerte ya que partiendo de esta premisa, podemos afirmar que en una dispersión socioeconómica con sesgo a la derecha, el número total de personas con un nivel económico que exceda la mediana es siempre menor, lo cual es desafortunadamente compatible con la mayoría de las sociedades. Entremos de lleno en el modelo y afirmemos que la dispersión de nuestra población está dada por una función densidad denominada: f(x), dicha función solamente debe cumplir la condición de tener un dominio conformando por R+ en el intervalo [w,y]. En dicho intervalo se encuentran todas las posibles posturas, las que representamos como: Ei . El conjunto Ei, desde la óptica de los jugadores es su conjunto de estrategias, en cuanto al número de jugadores, el modelo da cabida a un número n de jugadores (donde n ε N) de manera simultánea, cada jugador tendrá un beneficio dado por el número de votos, cuya totalidad en el modelo estará dada por: ∫uw f(x)1, , de esto se desprende que el número de votos del Ji puede expresarse de forma gráfica como un área “Ai” dada por: ∫m1m1-1 f(x), donde mi-1 es la media entre la estrategia del Ji-1 y el Ji mientras que, mi es la media entre la estrategia del Ji+1 y el Ji (Salvo J1 y Jn cuyas integrales estarán definidas por los intervalos [0, m1] y [mn-1, y], respectivamente), véase figura 3.2. Al igual que en los modelos de elecciones antes analizados, una de las características de los equilibrios de Nash de este modelo, es que en el punto de equilibrio, el número de votos (porcentaje en este caso), que recibe cada candidato es el mismo, por lo que el equilibrio de Nash para “n” jugadores cumple: Π1 = Π2 = ... Πn ó Siendo los elementos: f(x), “y” , “w” y “n”, determinados por la persona que use el modelo, podemos despejar en orden las “m”, ya que el beneficio de equilibrio puede ser conocido por 1/n ∫ yw f(x), de ahí que igualamos la integral definida que nos da el valor de Π1 , al valor conocido del beneficio de equilibrio para despejar m1 , la que sustituimos en el siguiente término y así de forma sucesiva hasta conocer todas las m, ya teniendo todas las m, basta con recordar que son las medias del valor de las estrategias para obtener un sistema de n ecuaciones con n incógnitas el cual una vez resuelto, nos dará el valor de las posturas que conforman el equilibrio de Nash, el hecho de que exista un sistema de n ecuaciones las con n incógnitas que determinan el equilibrio de Nash significa que existe un único equilibrio de Nash para cada número n de jugadores. esuelto nuestro modelo de la parte matemática, nos damos cuenta que llegar al equilibrio de Nash implica un alto nivel de esfuerzo 1 , a tal grado de volverse casi imposible si usamos funciones de densidad complejas, sin embargo como ya mencioné en la sección pasada el equilibrio de Nash en la realidad del modelo casi imposible, lo único importante del procedimiento era demostrar que para cualquier f (x) utilizada como función densidad a cada número de jugadores, existe únicamente un equilibrio de Nash2 , sin lo cual no podría estar completo el modelo. En la sección pasada se explicó el modelo en forma general, lo que creo pertinente a manera de conclusión, es brindar al lector ciertas reflexiones acerca de la forma de cómo utilizar el modelo, claro mientras sea utilizado siguiendo las premisas de la sección anterior. Antes de escribir este ensayo, tenía en mente la idea de crear un modelo que siguiera la lógica económica, similar al del teorema del votante mediano, que a la vez nos permitiera analizar otro tipo de situaciones, de ahí, fue donde surgió la idea general del modelo propuesto, esta idea general incluía (claro que aun no con tanto refinamiento) los elementos ya descritos en la sección anterior, sin embargo, lo que me hacia reflexionar, era la idea ( tal vez por mi formación como economista) de poder cuantificar (a través de un análisis basado en sus políticas , propuestas, discursos, etc.), la postura de una figura pública y de esta forma ser integrada en el modelo, donde también se usaría una función de densidad, que guardase proporciones similares a las de la sociedad en donde se desempeña dicho candidato. Al llevar a cabo estas afirmaciones, tenía en mente, hasta cierto punto, la forma en cómo los economistas pueden cuantificar las preferencias de un consumidor. Es así que, continuando con este razonamiento conocía la imposibilidad de que los candidatos en el mundo real llegaran a un equilibrio de Nash según el modelo (en la realidad alguien tiene que ganar), sin embargo, esto no descartaba la idea de utilizar el modelo para dar un parámetro de la postura que podría mejorar 3 la situación actual de los candidatos. Otra idea que tenía en mente, era la de poder explicar determinadas situaciones, por ejemplo, una situación donde el nivel socioeconómico cambie en cualquier dirección, la población tendería a sesgarse respecto a su posición inicial (funciones como beta y gama nos permiten hacer esto sin modifica nuestro intervalo), lo cual mostraría claramente como la población estaría dispuesta a seguir a una figura política de una posición más radical, como ha llegado a suceder en la historia. Con esta última reflexión, dejo a discreción del lector manera de interpretación del modelo que le parezcan rescatables, así como los grados de exactitud que esté dispuesto a darle, solamente esperando que haya disfrutado mi trabajo, como yo lo hice al escribirlo. Autor: Axel Chávez Gódinez Referencias - Novales, Alfonso, Estadística y econometría, Mc GrawHill.Madrid, 1997, 638 pp. - Dixit, Avinash y Nalebuff, Barry, Pensar estratégicamente, 3ra edición. Madrid, editorial Antoni Bosch, 1991, 416 pp. - Polak, Benjamin, “Yale Courses”, sesiones 3 y 7. [disponibleen:http://oyc.yale.edu/economics/game-theory/contents/sessions.html] - Nash, John,Tésis: Non cooperative Games, imprenta de Princeton, 1951. - Gibbons, Robert,Un primer curso de teoría de juegos, editorial Antoni Bosch, 1992, 288 pp. 1 - Nota: solo para darnos una idea, la función densidad que utilizó para ejemplificar en esta sección, es una función de densidad Gamma (?=2, ?=15 intervalo 0 a 50) aun que es fácilmente integrable, la ecuación donde se encuentra el equilibrio de Nash para “n=2”, no es despejable por métodos tradicionales. 2 - Observación: el resultado propuesto en esta última sección, es tan fuerte que, si como función densidad, utilizamos una constante (volvemos a una dispersión uniforme), a la cual aplicamos el procedimiento descrito, podemos encontrar algunos equilibrios de Nash del segundo modelo, no podemos encontrar todos por que en dicho modelo los jugadores no pueden elegir posición en la recta lo cual amplía el número de puntos que cumplen con la definición de equilibrio de Nash. 3- Nota: aunque en el modelo, no descarto, la idea de jugadores que eligen una postura, sería absurdo creer que en la realidad dicha postura puede cambiar tan constante y radicalmente como en el modelo, por lo que aplicado a la realidad, solo podría darnos un parámetro de la dirección de la mejor postura a seguir en campaña.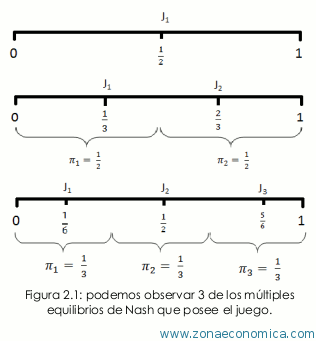
Figura 1.2: Eliminación iterativa de estrategias estrictamente dominadasModelo de elecciones políticas: Para una población con sesgos en su dispersión
Los individuos dentro de una población, fijan su postura política de acuerdo a su forma de pensar, la cual (para efectos del modelo) es acorde a su nivel socioeconómico
.
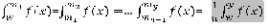
Conclusiones
zonaeconomica.com "Modelo de Elecciones Políticas: Para una Población con Sesgos de Dispersión" [en linea]
Dirección URL: https://www.zonaeconomica.com/modelo-de-elecciones-politicas (Consultado el 12 de Mar de 2026)
| Adjunto | Tamaño |
|---|---|
| 3.08 KB | |
| 7.06 KB | |
| 5.12 KB | |
| 14.25 KB | |
| 2.51 KB | |
| 3.54 KB | |
| 8.01 KB |