Producto Total, Medio y Marginal
Las empresas utilizan factores de producción o insumos, para elaborar productos y ofrecer servicios. Una función de producción describe una relación entre la cantidad de uno o varios insumos, y la cantidad producida, dada una determinada tecnología.
Cuando una función de producción se expresa con una fórmula matemática, generalmente se trata de modelos o construcciones teóricas, que nos permiten analizar situaciones y extraer conclusiones generales, a pesar de que se trate de una construcción teórica.
Un ejemplo de una función de producción puede ser el siguiente:
Q = L0.6 K0.4
Donde:
- Q es la cantidad producida
- T es la cantidad de horas hombre insumidas en la producción
- K es la cantidad de capital aplicado a la producción
Producto Total
El Producto Total es simplemente la cantidad de bienes producidos por todos los trabajadores e insumos aplicados a la producción.
Gráficamente: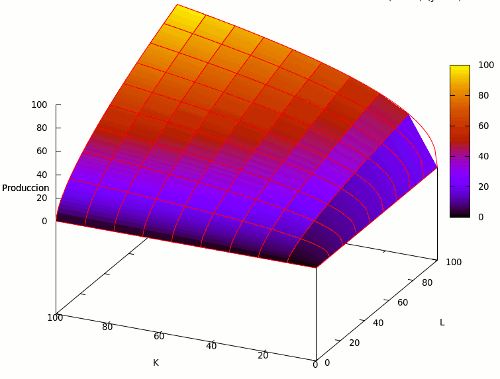
Producto Total = Cantidad de Bienes Producidos
Si fijamos el valor de uno de los dos insumos, por ejemplo, el capital en 50, podemos obtener el siguiente gráfico:
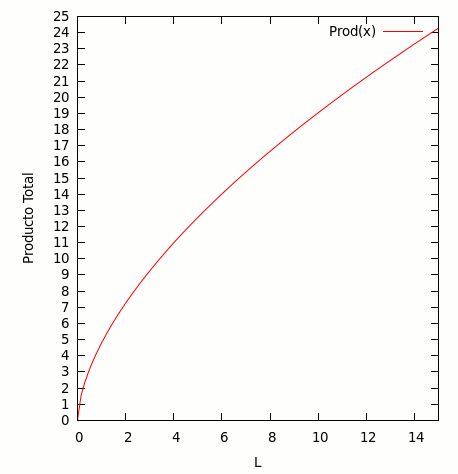
Esto equivaldría a "cortar" el primer gráfico en 3 dimensiones, en una recta paralela al eje "K", en el valor de 50 unidades de capital.
Esta situación, en la que uno de los factores se encuentra fijo, se denomina "de corto plazo", porque se supone que en el largo plazo, la cantidad de todos los factores es variable, mientras que en el corto plazo hay ciertos factores de producción que no se pueden modificar. Usualmente se considera al trabajo como variable en el corto plazo, mientras que el capital es sólo variable en el largo plazo.
Producto Medio
El producto medio se define como la cantidad promedio producida, por cada unidad de un determinado factor. Si este factor es el trabajo, es producto medio es el promedio producido por cada trabajador. Para obtener el producto medio debemos dividir el producto total, por la cantidad utilizada del factor.
Producto Medio = Cantidad de Bienes Producidos / Cantidad del Factor Utilizada
En nuesto ejemplo, si K=50 y L=10, el producto total es:
Q = L0.6 K0.4
Q = 100.6 500.4 = 19.04
En este caso, el producto medio del trabajo es 19.04 / 10 = 1.904 , es decir, que cada trabajador produce en promedio 1.904 unidades del bien.
Gráficamente:

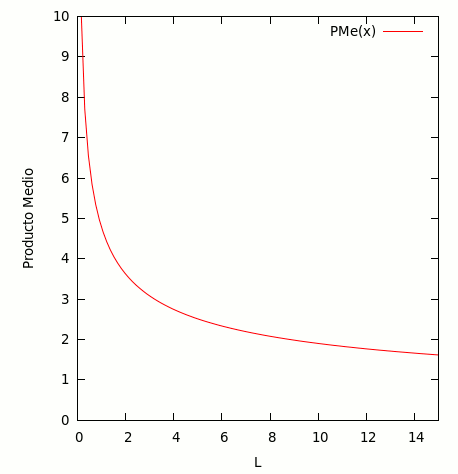
Producto Marginal
El producto marginal se define como el aumento del producto total, cuando se aumenta la cantidad utilizada de un insumo en una unidad.
Matemáticamente se puede describir de dos formas:
a) Cuando el análisis es discreto, se describe matemáticamente de la siguiente forma:
Producto Marginal = ΔQ / ΔL
b) Si el análisis es infinitesimal, se describe como:
Producto Marginal = dQ / dL
En nuestro caso, derivamos Q con respecto a L y obtenemos:
dQ/dL = 0.6 L-0.4 K0.4
Gráficamente:

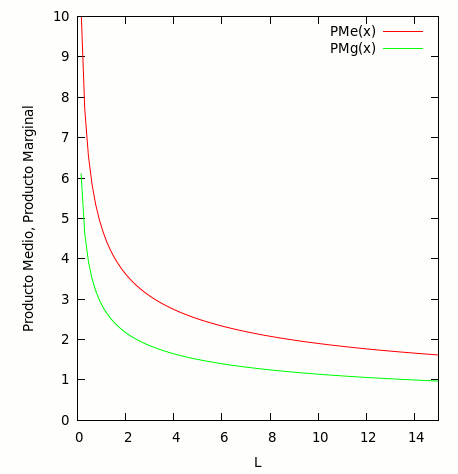
El gráfico nos muestra en la linea roja, el producto medio del trabajo, y en la linea verde, el producto marginal del trabajo.
Veamos un ejemplo numérico:
| Producto Total . | Horas de Trabajo | Producto Medio | Producto Marginal |
|---|---|---|---|
| 0 | 0 | ||
| 10 | 17 | 0.59 | 0.59 |
| 20 | 28 | 0.71 | 0.91 |
| 30 | 35 | 0.86 | 1.43 |
| 40 | 40 | 1.00 | 2.00 |
| 50 | 45 | 1.11 | 2.00 |
| 60 | 52 | 1.15 | 1.43 |
| 70 | 63 | 1.11 | 0.91 |
| 80 | 80 | 1.00 | 0.59 |
| 90 | 105 | 0.86 | 0.40 |
| 100 | 140 | 0.71 | 0.29 |
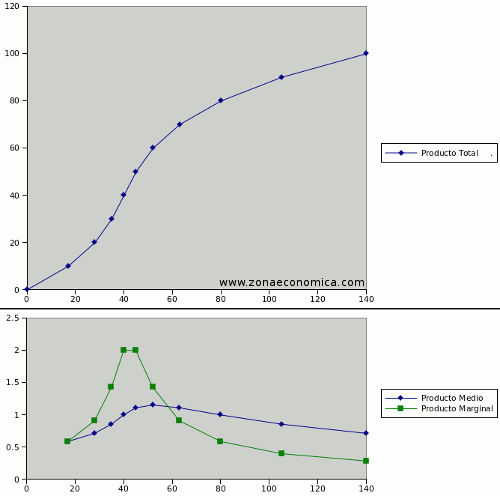
La linea verde nos muestra el producto marginal del trabajo y la azul, el producto medio del trabajo.
Análisis Gráfico
Como dijimos anteriormente, el producto medio, es la cantidad total producida dividida por la cantidad de trabajo. En el gráfico, podemos ver esto como la altura de la función en un punto, o la distancia de ese punto al eje "X", dividida la distancia de ese punto al eje "Y". Si trazamos un rayo que va desde el punto (0,0) hasta un punto sobre la función de producción, la pendiente de ese rayo, será la altura del punto dividida la distancia del punto al eje "X", es decir, la pendiente del rayo es el producto medio.
Si trazamos una recta tangente en la función de producción, la pendiente de esa recta será la derivada parcial de la función de producción con respecto al insumo, es decir, la pendiente de la recta tangente a la función de producción es la productividad marginal del insumo en cuestión.
Relación entre producto total, medio y marginal
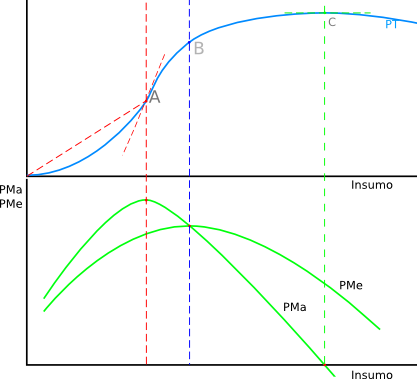
En el punto A, la pendiente de la función de producción es superior a la pendiente del rayo. La productividad marginal es superior a la productividad media.
En el punto B, ambas pendientes son iguales: la productividad marginal es igual a la productividad media. A partir del punto B, la productividad marginal es inferior a la productividad media: la productividad media comienza a descender.
En el punto C, la pendiente de la función de producción es cero: la productividad marginal es cero. A partir del punto C, la productividad marginal es negativa: el producto total comienza a descender.
Federico "Producto Total, Medio y Marginal" [en linea]
Dirección URL: https://www.zonaeconomica.com/producto-total-medio-marginal (Consultado el 13 de Mar de 2026)
 En la teoría microeconómica neoclásica, una función de producción es la expresión matemática que describe la relación entre la cantidad de insumos utilizados y la cantidad unidades de un producto obtenido, en...
En la teoría microeconómica neoclásica, una función de producción es la expresión matemática que describe la relación entre la cantidad de insumos utilizados y la cantidad unidades de un producto obtenido, en...